MathC2+ (Jérôme BASTIEN)
-
-
2017 : Parabole et circuits de train
Nous construirons une parabole ; elle sera utilisée pour construire des rails de circuits de train.
-
Déroulement
-
Conférence : une petite présentation succincte de la modélisation et de l'effet Magnus sera faite.
-
Atelier parabole
-
Nous utiliserons des programmes permettant de créer des plans de circuits. Ces programmes, distribués pour Windows, sont diponibles :
-
-
2016 : Parabole et circuits de train
Plus encore que l'année dernière, l'accent sera mis sur la parabole, sous toutes ses formes ; elle sera utilisée pour construire des rails de circuits de train.
-
Déroulement
-
Conférence 1 : une petite présentation succincte de la modélisation et de l'effet Magnus sera faite.
-
Atelier 1 : cet atelier sera consacré à la construction de pièces du circuit de train, étudié dans le détail par la suite.
On construira en particulier une parabole de façon purement géométrique et qui servira dans le circuit de train.
Voir le texte.
Cet atelier est inspiré des annexes G et H du cours de L2 en biomécanique
qui sont un peu plus détaillées.
-
Conférence 2 : Le circuit de train étudié.
Transparents présentés, sensiblement les mêmes que ceux présentés
lors de la semaine
"les mathématiques nous transportent!"
-
Atelier 2 : problème d'énumération de circuits.
-
Nous utiliserons des programmes permettant de créer des plans de circuits. Ces programmes, distribués pour Windows, sont diponibles :
- Ensemble des Scripts GeoGebra utilisés (Merci à Christian Mercat !)
-
-
2015 : La parabole, sports et jeux
Plusieurs choses seront traitées dans cette thématique :
-
Une petite présentation succincte de la modélisation en biomécanique sera faite.
-
Ensuite, un atelier sera consacré à la parabole et à l'effet Magnus au football. Une petite promenade à travers les siècles vous permettra
de construire la parabole de la chute libre et de montrer comment le ballon passe au-dessus du mur de joueurs. Ensuite, une construction
aidée par les programmes fournis vous permettra de comprendre pourquoi l'effet Magnus et le frotté du ballon lui permettent de rentrer dans la cage des buts.
-
Une seconde utilisation ludique de la parabole, dans le cadre d'un jeux breveté, sera traitée sous la forme d'un atelier .
- plus de détails sur ce jeu
- Transparents présentés, sensiblement les mêmes que ceux présentés
lors de la semaine
"les mathématiques nous transportent!"
- J'apporterai les prototypes des rails construits et vous aurez l'occasion de jouer avec de vraies paraboles !
- Enfin, nous utiliserons des programmes permettant de créer des plans de circuits.
-
Ces programmes, distribués pour Windows, sont diponibles :
-
Un catalogue
présente quelques circuits contenant au maximum 4 pièces par type, soit au total 24 pièces.
Pages 317 à 361 de ce catalogue, sont présentés 45 circuits à 17 pièces, déterminés aléatoirement,
grâce au programme creecircuitaleat.exe.
Aux pages 375 et 376 sont présentés deux circuits à 18 et 20 pièces,
déterminés manuellement. Enfin, aux pages 377 et 378 sont présentés deux circuits
maximaux, c'est-à-dire contenant toutes les pièces ! Mais ces deux derniers
circuits présentent certaines symétries, ce qui a permis de les construire.
-
Jeu du jour : En utilisant le logiciel creecircuit.exe
ou avec les prototypes fournis (30 pièces), seriez-vous capables de déterminer
d'autres circuits les plus grands possibles, à 24 ou 30 pièces ?
-
Solutions trouvées : Bravo à vous qui avez trouvé les circuits suivants (avec les logiciels ou les rails) :
- Manon et Amandine (29 pièces sur 30) :


- Roxana (28 pièces sur 30) :

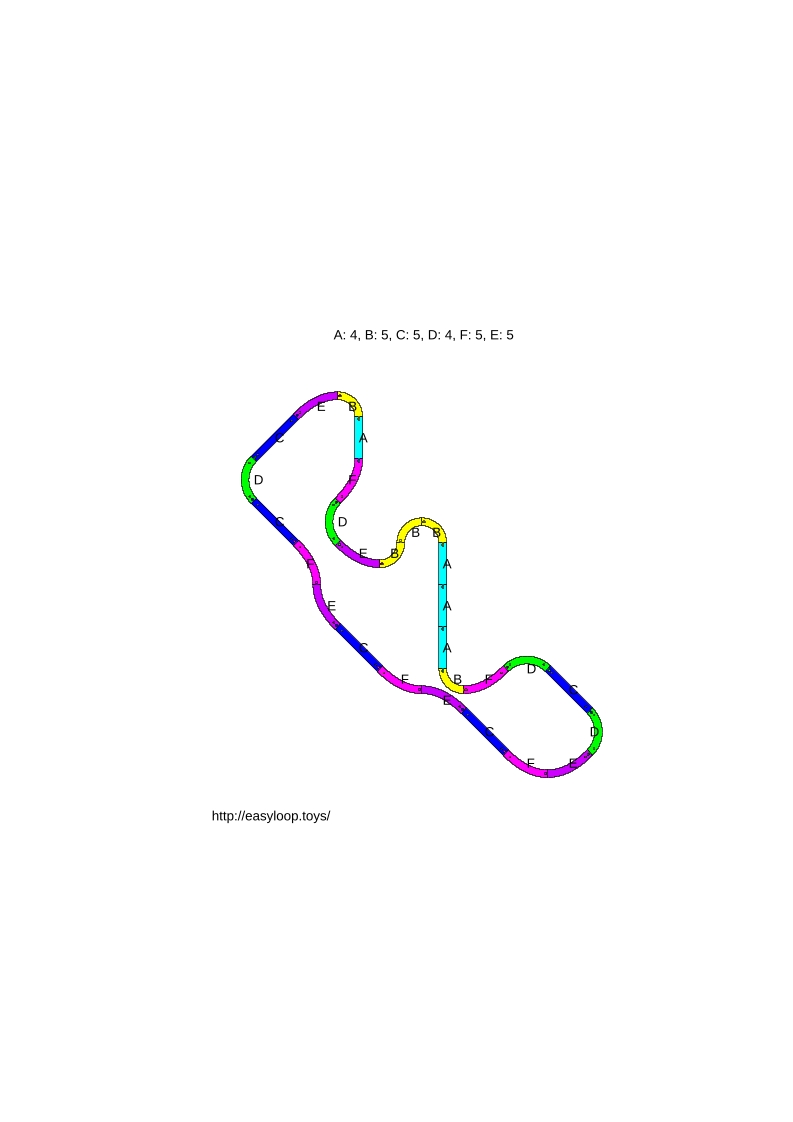
- Alexis, Douna et Ségolène (22 pièces sur 24) :
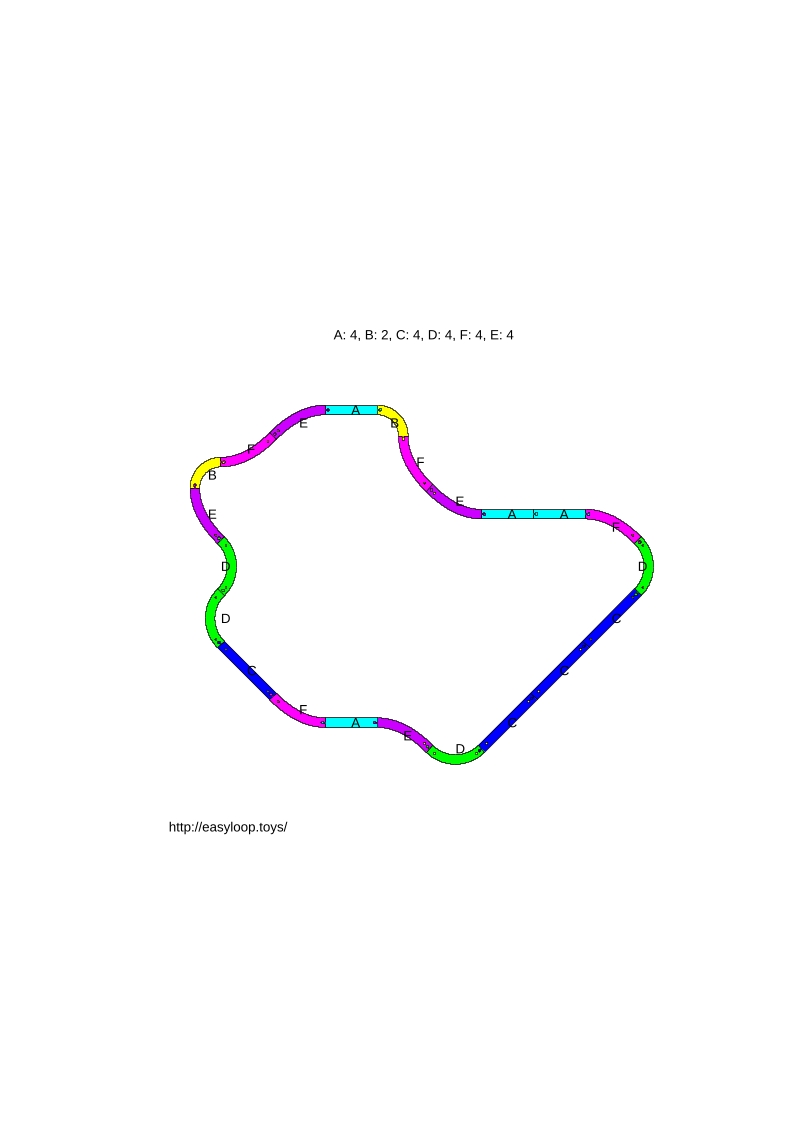


- l (21 pièces sur 24) :
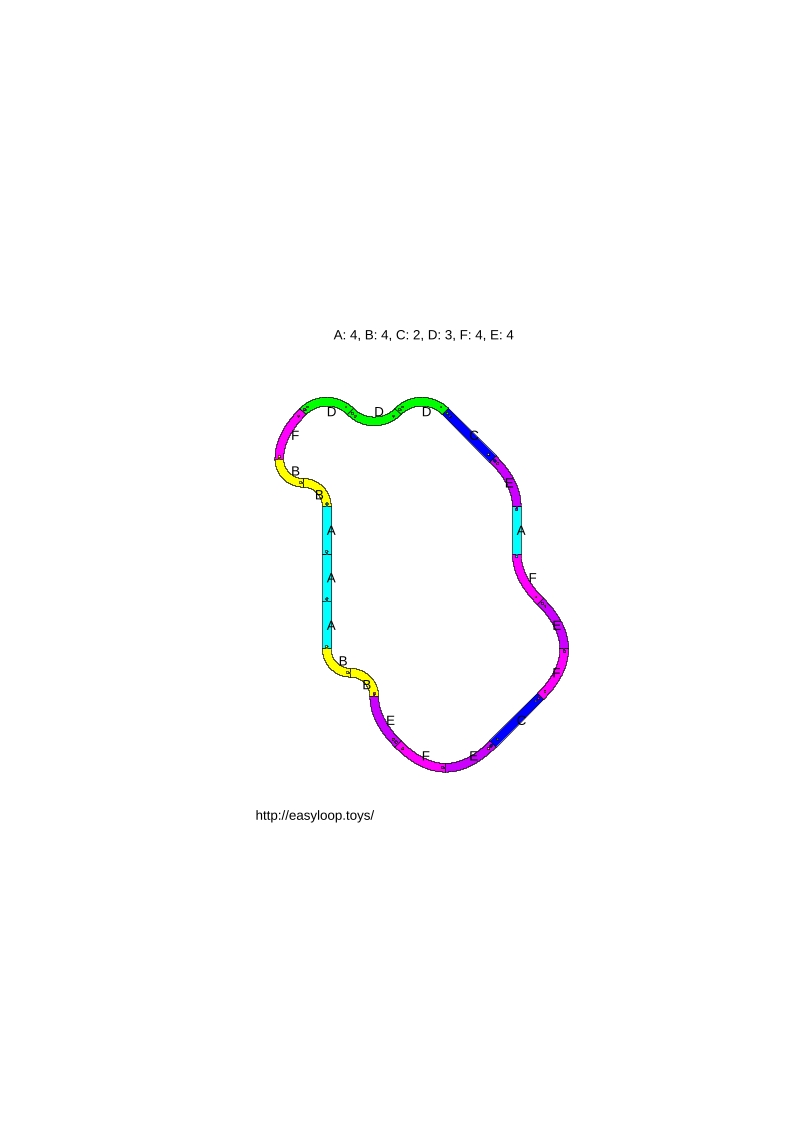
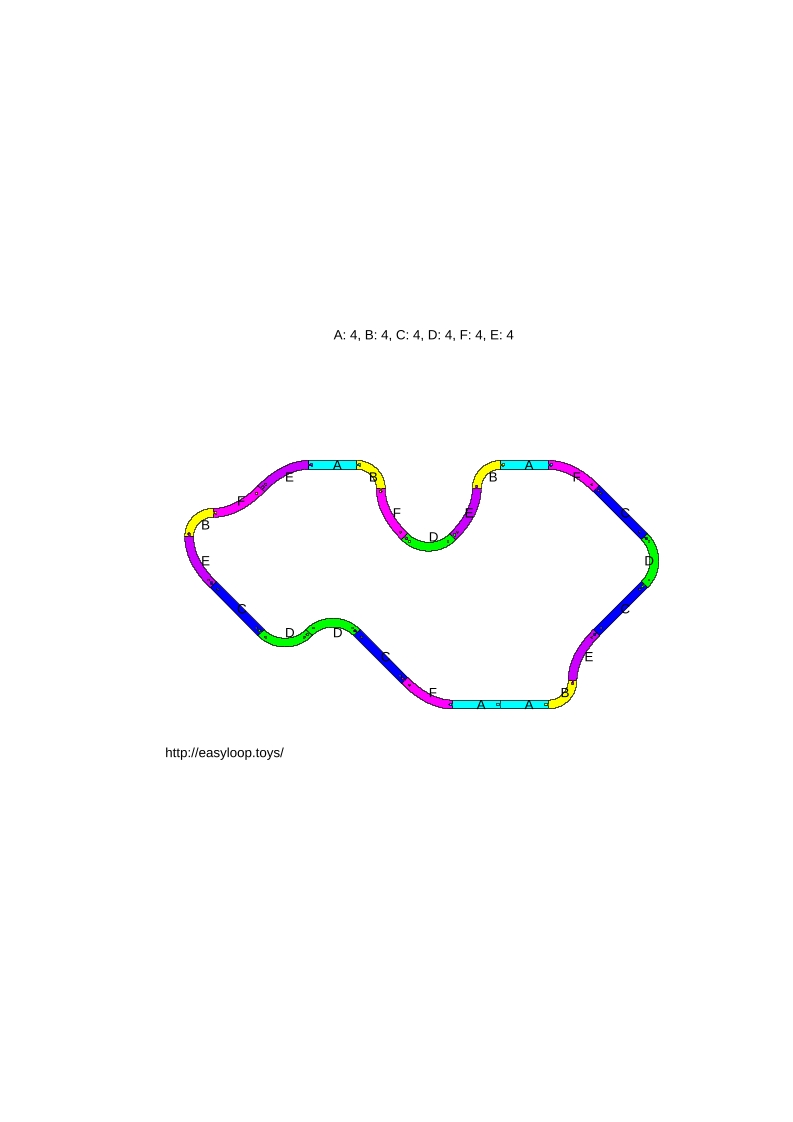
- Youdanou (20 pièces sur 24) :

- Et pour finit, merci à Douna, puisqu'en rajoutant 2 pièces à son circuit, on obtenait un circuit maximal de 24 pièces !
Retour









